|
|
|
|
Курсовая: Динамическое и линейное программирование
Таблица 5. | 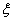
| 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | | 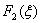
| 0 | 42 | 72 | 91 | 107 | 121 | 134 | 143 | | 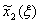
| 0 | 0 | 100 | 200 | 200 | 300 | 300 | 300 | |
Для заполнения таблицы 7 необходимо в таблице 6 сложить значения функции 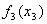 со значениями
со значениями 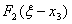 и на
каждой северо-восточной диагонали выбрать наибольшее число (отмечено
звездочкой), указав соответствующие значение и на
каждой северо-восточной диагонали выбрать наибольшее число (отмечено
звездочкой), указав соответствующие значение 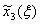 :
:
Таблица 7. | 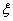
| 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | | 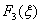
| 0 | 42 | 72 | 94 | 113 | 129 | 144 | 158 | | 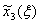
| 0 | 0 | 0 | 100 | 100 | 100 | 200 | 200 | |
Теперь, в таблице 8, необходимо сложить значения функции 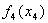 со значениями
со значениями 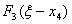 , но
только для значения , но
только для значения 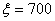 , т.е. заполнить только одну диагональ:
, т.е. заполнить только одну диагональ:
Таблица 8. | 
| 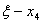
| 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 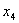
| 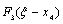
| 0 | 42 | 72 | 94 | 113 | 129 | 144 | 158 | 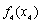
|  0 0
| 0 | | | | | | | | 158 |      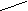 100 100
| 50 | | | | | | | 194 | | | 200 | 68 | | | | | | 197* | | | | 300 | 82 | | | | | 195 | | | | | 400 | 92 | | | | 186 | | | | | | 500 | 100 | | | 172 | | | | | | | 600 | 107 | | 149 | | | | | | | | 700 | 112 | 112 | | | | | | | |
Наибольшее число этой диагонали показывает максимально возможный суммарный
прирост прибыли всех четырех предприятий данного производственного
объединения, при общей сумме капитальных вложений в 700 денежных единиц,
т.е.:
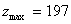 денежных единиц
причем четвертому предприятию должно быть выделено: денежных единиц
причем четвертому предприятию должно быть выделено:
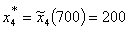 денежных единиц
Тогда третьему предприятию должно быть выделено (см. табл. 7.): денежных единиц
Тогда третьему предприятию должно быть выделено (см. табл. 7.):
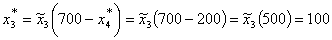 денежных единиц
второму предприятию должно быть выделено (см. табл. 5.): денежных единиц
второму предприятию должно быть выделено (см. табл. 5.):
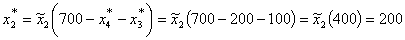 денежных единиц
на долю первого предприятия остается:
денежных единиц
на долю первого предприятия остается:
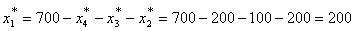 денежных единиц
Таким образом, наилучшим является следующее распределение капитальных
вложений по предприятиям: денежных единиц
Таким образом, наилучшим является следующее распределение капитальных
вложений по предприятиям:
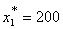 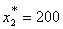 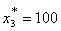 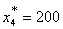 которое обеспечивает производственному объединению наибольший возможный
прирост прибыли:
которое обеспечивает производственному объединению наибольший возможный
прирост прибыли:
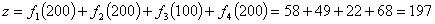 денежных единиц
денежных единиц
6. Динамическая задача управления запасами
Задача управления запасами – это задача о поддержании баланса производства и
сбыта продукции предприятия, минимизирующего расходы предприятия на
производство и хранение продукции.
Предположим, что предприятие, производящее партиями некоторую продукцию,
получило заказы на n месяцев. Размеры заказов значительно меняются от
месяца к месяцу, поэтому иногда лучше выполнять заказы сразу нескольких
месяцев, а затем хранить готовую продукцию, пока она не потребуется, чем
выполнять заказ именно в тот месяц, когда этот заказ должен быть отправлен.
Поэтому необходимо составить план производства на эти n месяцев с
учетом затрат на производство и хранение изделий.
Примем следующие обозначения:
| Номер месяца (j=1,2,.,n) | 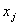
| Число изделий, производимых в j-ом месяце | 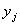
| Величина запаса к началу j-го месяца | 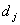
| Число изделий, которые должны быть отгружены в j-ом месяце | 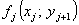
| Затраты на хранение и производство изделий в j-ом месяце |
Тогда, задача состоит в том, чтобы найти план производства 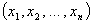 компоненты которого удовлетворяют условиям материального баланса:
компоненты которого удовлетворяют условиям материального баланса:
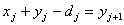 , где , где 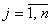 и минимизируют суммарные затраты за весь планируемый период:
и минимизируют суммарные затраты за весь планируемый период:
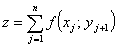 причем по смыслу задачи
причем по смыслу задачи 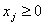 , , 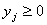 , при , при 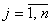 Т.к. объем произведенной продукции
Т.к. объем произведенной продукции 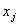 на этапе j может быть настолько велик, что запас
на этапе j может быть настолько велик, что запас 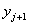 может удовлетворить спрос всех последующих этапов и при этом не имеет смысла
иметь величину запаса
может удовлетворить спрос всех последующих этапов и при этом не имеет смысла
иметь величину запаса 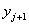 больше суммарного спроса на всех последующих этапах, то переменная
больше суммарного спроса на всех последующих этапах, то переменная 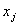 должна удовлетворять ограничениям:
должна удовлетворять ограничениям:
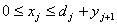 Полученную задачу можно решить методом динамического программирования, для чего
необходимо определить параметр состояния
Полученную задачу можно решить методом динамического программирования, для чего
необходимо определить параметр состояния 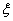 и функцию состояния
и функцию состояния 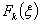 :
:
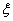
| Наличный запас продукции в конце k-го месяца (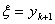 ) ) | 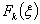
| Минимальные затраты за первые 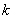 месяцев: месяцев: 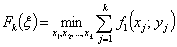 |
Тогда, минимальные затраты за один первый месяц (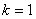 ): ):
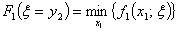 Следовательно, минимальные затраты при
Следовательно, минимальные затраты при 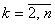 : :
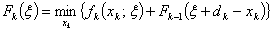 , где , где 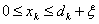 Если при этом функция затрат на хранение и производство изделий в j-ом месяце
имеет вид:
Если при этом функция затрат на хранение и производство изделий в j-ом месяце
имеет вид:
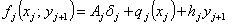 , где , где
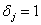 , при , при 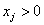 и и 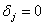 , при , при 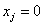
| 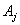
| Затраты на оформление заказа (переналадку оборудования) в j-ом месяце | 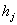
| Затраты на хранение единицы продукции, переходящей из j‑го месяца в месяц j+1 | 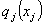
| Затраты на производство (закупку) 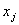 единиц продукции в j‑ом месяце единиц продукции в j‑ом месяце |
то минимальные затраты за один первый месяц (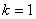 ): ):
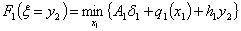 если ввести обозначение:
если ввести обозначение:
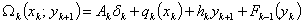 то следовательно, минимальные затраты при
то следовательно, минимальные затраты при 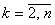 : :
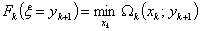 , где , где 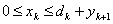 Допустим, что предприятие заключило договора на поставку своей продукции на три
месяца. Исходные данные приведены в таблице 9. При этом исходный запас товара
на складе составляет две единицы, т.е
Допустим, что предприятие заключило договора на поставку своей продукции на три
месяца. Исходные данные приведены в таблице 9. При этом исходный запас товара
на складе составляет две единицы, т.е 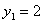 .
.
Таблица 9. | Период k | 1 | 2 | 3 | Спрос (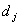 ) ) | 3 | 2 | 3 | Затраты на оформление заказа (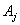 ) ) | 4 | 2 | 3 | Затраты на хранение единицы запаса (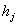 ) ) | 1 | 1 | 1 |
Предполагается, что затраты на приобретение продукции составляют 5 руб. за
каждую единицу для первых трех единиц и 7 руб. за каждую дополнительную
единицу, т.е.
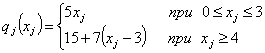 Положим
Положим 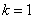 , тогда: , тогда:
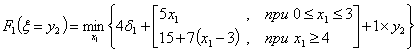 Тогда, т.к. параметр состояния
Тогда, т.к. параметр состояния 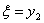 может принимать значения на отрезке: может принимать значения на отрезке:
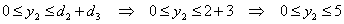 т.е.
т.е. 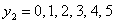 , при этом
каждому значению параметра состояния отвечает определенная область изменения
переменной , при этом
каждому значению параметра состояния отвечает определенная область изменения
переменной 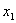 : :
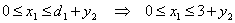 Однако на первом этапе объем производства не может быть меньше одной единицы,
т.к. спрос
Однако на первом этапе объем производства не может быть меньше одной единицы,
т.к. спрос 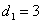 , а
исходный запас , а
исходный запас 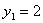 ,
при этом из балансового уравнения следует, что объем производства связан с
параметром состояния ,
при этом из балансового уравнения следует, что объем производства связан с
параметром состояния 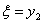 соотношением:
соотношением:
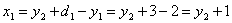 т.е. каждому значению
т.е. каждому значению 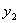 отвечает единственное значение отвечает единственное значение 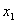 , поэтому: , поэтому:
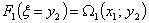 , тогда:
Значения функции состояния , тогда:
Значения функции состояния 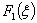 приведены в таблице 10.: приведены в таблице 10.:
Таблица 10. | 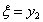
| 0 | 1 | 2 | 3 | 4 | 5 | 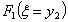
| 9 | 15 | 21 | 29 | 37 | 45 | 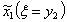
| 1 | 2 | 3 | 4 | 5 | 6 |
Положим  , тогда: , тогда:
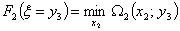 , где: , где:
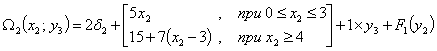 Здесь минимум берется по переменной
Здесь минимум берется по переменной 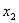 , которая может изменяться в пределах: , которая может изменяться в пределах:
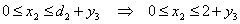 где верхняя граница зависит от параметра состояния
где верхняя граница зависит от параметра состояния 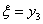 , который принимает значения на отрезке:
, который принимает значения на отрезке:
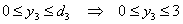 т.е.
т.е. 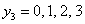 , при этом из
балансового уравнения следует, что остаток товара на начало второго месяца , при этом из
балансового уравнения следует, что остаток товара на начало второго месяца 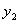 связан с объемом производства
связан с объемом производства 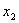 и с параметром состояния
и с параметром состояния 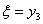 соотношением:
соотношением:
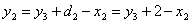 Тогда:
Наименьшие из полученных значений
Тогда:
Наименьшие из полученных значений 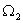 , есть , есть 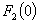 , т.е.: , т.е.:
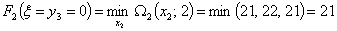 причем минимум достигается при
причем минимум достигается при 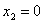 и и 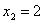 , т.е.: , т.е.:
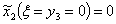 и и 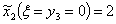 эти значения указываем в результирующей таблице 11.
Аналогично:
Таким образом:
эти значения указываем в результирующей таблице 11.
Аналогично:
Таким образом:
Таблица 11. | 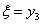
| 0 | 1 | 2 | 3 | 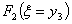
| 21 | 27 | 34 | 41 | 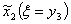
| 0 | 2 | 3 | 3 | 3 | | | | | | |
Теперь положим, что 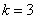 , тогда: , тогда:
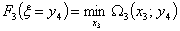 , где: , где:
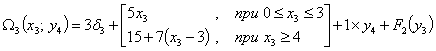 Если оставлять продукцию к концу третьего периода не нужно, тогда параметр
состояния принимает единственное значение
Если оставлять продукцию к концу третьего периода не нужно, тогда параметр
состояния принимает единственное значение 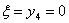 , следовательно, переменная
, следовательно, переменная 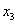 может изменяться в пределах:
может изменяться в пределах:
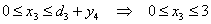 а из балансового уравнения следует, что остаток товара на начало третьего месяца
а из балансового уравнения следует, что остаток товара на начало третьего месяца 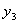 связан с объемом производства соотношением:
связан с объемом производства соотношением:
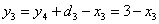 Тогда:
Следовательно, получаем:
Тогда:
Следовательно, получаем:
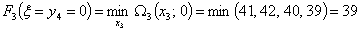 причем минимум достигается при
причем минимум достигается при 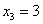 , т.е.: , т.е.:
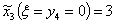 Таким образом, получили минимальные общие затраты на производство и хранение
продукции и последнюю компоненту оптимального решения:
Таким образом, получили минимальные общие затраты на производство и хранение
продукции и последнюю компоненту оптимального решения:
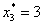 Для нахождения остальных компонент оптимального решения, необходимо
воспользоваться обычными правилами динамического программирования.
Тогда т.к.
Для нахождения остальных компонент оптимального решения, необходимо
воспользоваться обычными правилами динамического программирования.
Тогда т.к. 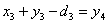 , то , то 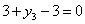 , откуда , откуда 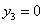 , следовательно, из таблицы 11.: , следовательно, из таблицы 11.:
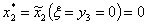 или или 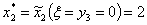 Аналогично т.к.
Аналогично т.к. 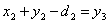 , то , то 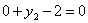 или или 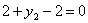 , откуда , откуда 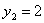 или или 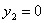 , следовательно, из таблицы 10.: , следовательно, из таблицы 10.:
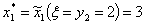 или или 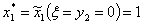 Следовательно, получен оптимальный план производства, который имеет два
варианта:
при этом, каждый вариант оптимального плана производства обеспечивает
минимальные общие затраты на производство и хранение продукции в размере 39
денежных единиц.
Следовательно, получен оптимальный план производства, который имеет два
варианта:
при этом, каждый вариант оптимального плана производства обеспечивает
минимальные общие затраты на производство и хранение продукции в размере 39
денежных единиц.
7. Анализ доходности и риска финансовых операций
Финансовой называется операция, начальное и конечное состояние которой имеют
денежную оценку и цель проведения которой заключается в максимизации дохода в
виде разности между конечной и начальной оценками. При этом практически все
финансовые операции проходят в условиях неопределенности и, следовательно, их
результат невозможно предсказать заранее. Поэтому при проведении финансовой
операции возможно получение как прибыли, так и убытка.
Поэтому задача анализа доходности и риска финансовой операций заключается в
оценке финансовой операции с точки зрения ее доходности и риска. Наиболее
распространенным способом оценки финансовой операций является представление
дохода операции как случайной величины и оценка риска операции как среднего
квадратического отклонения этого случайного дохода.
Например, если доход от проведения некоторой финансовой операции есть случайная
величина 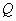 , то
средний ожидаемый доход , то
средний ожидаемый доход 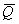 – это математическое ожидание случайной величины
– это математическое ожидание случайной величины 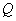 :
:
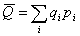 , где , где 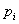 есть вероятность получить доход есть вероятность получить доход 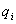 Т.к. среднеквадратическое отклонение:
Т.к. среднеквадратическое отклонение:
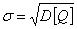 , где , где 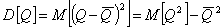 это мера разбросанности возможных значений дохода вокруг среднего ожидаемого
дохода, то его можно считать количественной мерой риска операции и обозначить
как
это мера разбросанности возможных значений дохода вокруг среднего ожидаемого
дохода, то его можно считать количественной мерой риска операции и обозначить
как 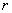 : :
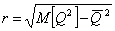 Допустим, что по четырем финансовым операциям
Допустим, что по четырем финансовым операциям 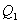 ,
, 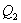 , , 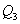 ,
, 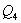 ряды
распределения доходов и вероятностей получения этих доходов имеют вид:
Тогда т.к. ряды
распределения доходов и вероятностей получения этих доходов имеют вид:
Тогда т.к. 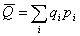 , то средний ожидаемый доход каждой операции имеет вид: , то средний ожидаемый доход каждой операции имеет вид:
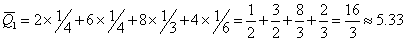
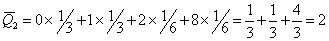
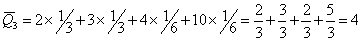
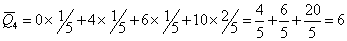 Т.к.
Т.к. 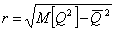 , то риски каждой финансовой операции имеют вид: , то риски каждой финансовой операции имеют вид:
 Нанесем средние ожидаемые
доходы Нанесем средние ожидаемые
доходы 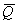 и риски и риски 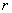 каждой операции на плоскость (см. график 2.).
Тогда, чем правее точка на графике, тем более доходная операция, чем точка
выше – тем более она рисковая.
Для определения операции оптимальной по Парето, необходимо на графике найти
точку, которую не доминирует никакая другая точка.
Так как точка
каждой операции на плоскость (см. график 2.).
Тогда, чем правее точка на графике, тем более доходная операция, чем точка
выше – тем более она рисковая.
Для определения операции оптимальной по Парето, необходимо на графике найти
точку, которую не доминирует никакая другая точка.
Так как точка 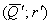 доминирует точку
доминирует точку 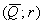 ,
если ,
если 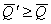 и и 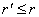 , то из графика 2. видно, что 3-ая операция доминирует 2-ую операцию, а 1-ая
операция доминирует 3-ую и 2-ую операции. Но 1-ая и 4-ая операции несравнимы,
т.к. доходность 4-ой операции больше, но и риск ее тоже больше, чем доходность
и риск 1-ой операции, следовательно, 1-я операция является оптимальной по
Парето.
Для нахождения лучшей операции можно применить взвешивающую формулу, которая для
пар
, то из графика 2. видно, что 3-ая операция доминирует 2-ую операцию, а 1-ая
операция доминирует 3-ую и 2-ую операции. Но 1-ая и 4-ая операции несравнимы,
т.к. доходность 4-ой операции больше, но и риск ее тоже больше, чем доходность
и риск 1-ой операции, следовательно, 1-я операция является оптимальной по
Парето.
Для нахождения лучшей операции можно применить взвешивающую формулу, которая для
пар 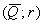 дает одно
число, по которому можно определить лучшую операцию. Допустим, что взвешивающей
формулой будет дает одно
число, по которому можно определить лучшую операцию. Допустим, что взвешивающей
формулой будет 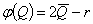 ,
тогда:
Отсюда видно, что 1-ая финансовая операция – лучшая, а 2-ая – худшая. ,
тогда:
Отсюда видно, что 1-ая финансовая операция – лучшая, а 2-ая – худшая.
8. Оптимальный портфель ценных бумаг
Задача о формировании оптимального портфеля ценных бумаг – это задача о
распределении капитала, который участник рынка хочет потратить на покупку
набора ценных бумаг, по различным видам ценных бумаг, удовлетворяющих
возможность получения некоторого дохода.
Из характеристик ценных бумаг наиболее значимы две: эффективность и
рискованность. Т.к. эффективность 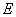 – это некоторый обобщенный показатель дохода или прибыли, то ее считают
случайной величиной, а ее математическое ожидание обозначают как
– это некоторый обобщенный показатель дохода или прибыли, то ее считают
случайной величиной, а ее математическое ожидание обозначают как 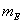 . Рискованность ценных бумаг отождествляют со средним квадратическим
отклонением, при этом дисперсию обычно называют вариацией и обозначают как
. Рискованность ценных бумаг отождествляют со средним квадратическим
отклонением, при этом дисперсию обычно называют вариацией и обозначают как 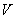 , т.е.:
, т.е.:
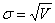 , где , где 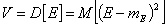 Примем следующие обозначения:
Примем следующие обозначения:
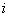
| Номер вида ценных бумаг | 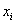
| Доля капитала, потраченная на закупку ценных бумаг i-го вида (сумма всех долей равна единице) | 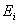
| Эффективность ценных бумаг i-го вида, стоящих одну денежную единицу | 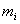
| Математическое ожидание эффективности 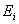 | 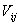
| Ковариация ценных бумаг i-го и j-го видов | 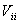
| Вариация (дисперсия) эффективности 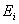 | 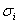
| Рискованность ценных бумаг i-го вида | 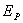
| Эффективность портфеля (набора) ценных бумаг |
Тогда, математическое ожидание эффективности портфеля ценных бумаг:
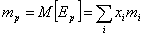 вариация портфеля ценных бумаг:
вариация портфеля ценных бумаг:
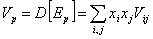 риск портфеля ценных бумаг:
риск портфеля ценных бумаг:
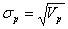 Следовательно, математическая формализация задачи формирования оптимального
портфеля ценных бумаг:
Найти такое распределение долей капитала, которое минимизирует вариацию
эффективности портфеля, при заданной ожидаемой эффективности портфеля
Следовательно, математическая формализация задачи формирования оптимального
портфеля ценных бумаг:
Найти такое распределение долей капитала, которое минимизирует вариацию
эффективности портфеля, при заданной ожидаемой эффективности портфеля 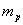 .
Тогда, если оптимальное решение обозначить как *, то:
.
Тогда, если оптимальное решение обозначить как *, то:
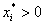
| означает рекомендацию вложить долю 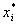 капитала в ценные бумаги i‑го вида капитала в ценные бумаги i‑го вида | 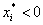
| Означает возможность проведения операции “short sale”, т.е. краткосрочного вложения доли капитала в более доходные ценные бумаги |
Если на рынке есть безрисковые ценные бумаги, то решение задачи о
формировании портфеля ценных бумаг приобретает новое качество.
Пусть:
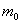
| Эффективность безрисковых ценных бумаг | 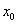
| Доля капитала, вложенного в безрисковые ценные бумаги | 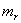
| Средняя ожидаемая эффективность рисковой части портфеля | 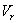
| Вариация рисковой части портфеля | 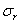
| Среднее квадратическое отклонение эффективности рисковой части портфеля |
Тогда в рисковую часть портфеля вложена 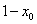 часть всего капитала, а т.к. считается, что безрисковые ценные бумаги
некоррелированы с остальными, то ожидаемая эффективность всего портфеля ценных
бумаг:
часть всего капитала, а т.к. считается, что безрисковые ценные бумаги
некоррелированы с остальными, то ожидаемая эффективность всего портфеля ценных
бумаг:
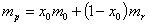 вариация портфеля ценных бумаг:
вариация портфеля ценных бумаг:
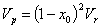 риск портфеля ценных бумаг:
риск портфеля ценных бумаг:
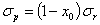 Допустим, что задача состоит в нахождении распределения капитала, при
формировании оптимального портфеля ценных бумаг заданной эффективности,
состоящего из трех видов ценных бумаг: безрисковых эффективности 3 и
некоррелированных рисковых, с ожидаемой эффективностью 5 и 9, риски которых
равны 4 и 6, т.е.:
Допустим, что задача состоит в нахождении распределения капитала, при
формировании оптимального портфеля ценных бумаг заданной эффективности,
состоящего из трех видов ценных бумаг: безрисковых эффективности 3 и
некоррелированных рисковых, с ожидаемой эффективностью 5 и 9, риски которых
равны 4 и 6, т.е.:
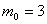 , , 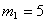 , , 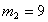 , , 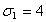 , , 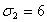 Тогда, вариации некоррелированных рисковых ценных бумаг первого и второго вида:
Следовательно, матрица
Тогда, вариации некоррелированных рисковых ценных бумаг первого и второго вида:
Следовательно, матрица 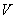 ковариаций рисковых видов ценных бумаг и вектор‑столбец
ковариаций рисковых видов ценных бумаг и вектор‑столбец 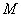 ожидаемой эффективности рисковых видов ценных бумаг имеют вид:
Пусть
ожидаемой эффективности рисковых видов ценных бумаг имеют вид:
Пусть 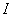 - двухмерный вектор-столбец, компоненты которого равны 1, т.е.: - двухмерный вектор-столбец, компоненты которого равны 1, т.е.:
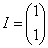 Тогда значение вектора-столбца
Тогда значение вектора-столбца 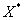 оптимальных значений долей, вложенных в рисковую часть портфеля ценных бумаг:
оптимальных значений долей, вложенных в рисковую часть портфеля ценных бумаг:
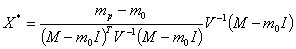 Где:
Где:
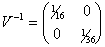
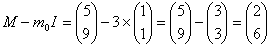
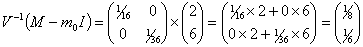
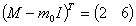
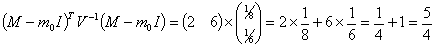 Т.е.:
Т.е.:
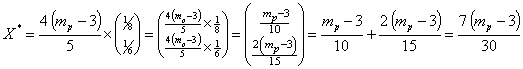 Таким образом, доли рисковых ценных бумаг в оптимальном портфеле:
Таким образом, доли рисковых ценных бумаг в оптимальном портфеле:
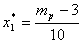 , , 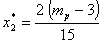 Следовательно, доля безрисковых ценных бумаг в оптимальном портфеле:
Следовательно, доля безрисковых ценных бумаг в оптимальном портфеле:
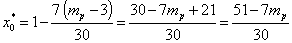 Т.к. необходимость проведения операции “short sale” возникает, когда
Т.к. необходимость проведения операции “short sale” возникает, когда 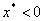 , то в данном случае, необходимость проведения операции “short sale” возникает,
когда
, то в данном случае, необходимость проведения операции “short sale” возникает,
когда 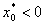 : :
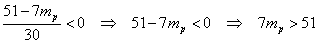 , т.е. когда , т.е. когда 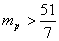 . .
Страницы: 1, 2, 3, 4
|
|
|
|
|

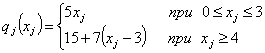 Положим
Положим 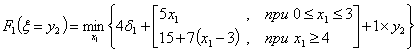 Тогда, т.к. параметр состояния
Тогда, т.к. параметр состояния 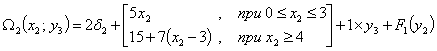 Здесь минимум берется по переменной
Здесь минимум берется по переменной 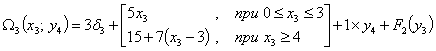 Если оставлять продукцию к концу третьего периода не нужно, тогда параметр
состояния принимает единственное значение
Если оставлять продукцию к концу третьего периода не нужно, тогда параметр
состояния принимает единственное значение  Нанесем средние ожидаемые
доходы
Нанесем средние ожидаемые
доходы 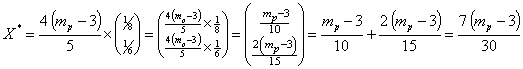 Таким образом, доли рисковых ценных бумаг в оптимальном портфеле:
Таким образом, доли рисковых ценных бумаг в оптимальном портфеле: