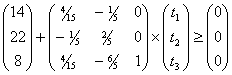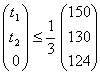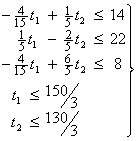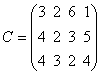|
|
|
|
Курсовая: Динамическое и линейное программирование
при условии сохранения структуры производственной программы:
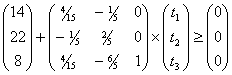
| (3.2) |
предполагая, что можно надеяться получить дополнительно не более одной трети
первоначального объема ресурса каждого вида, т.е.:
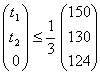
| (3.3) |
причем дополнительные объемы ресурсов, по смыслу задачи, не могут быть
отрицательными, т.е.:
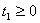 , , 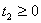
| (3.4) |
Т.к. неравенства (3.2) и (3.3) должны выполняться одновременно, то их можно
переписать в виде одной системы неравенств:
‚ ƒ „ … | 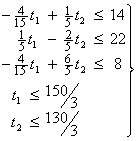
| (3.5) |
Таким образом, получена задача линейного программирования: максимизировать
функцию (3.1) при условиях (3.4) и (3.5).
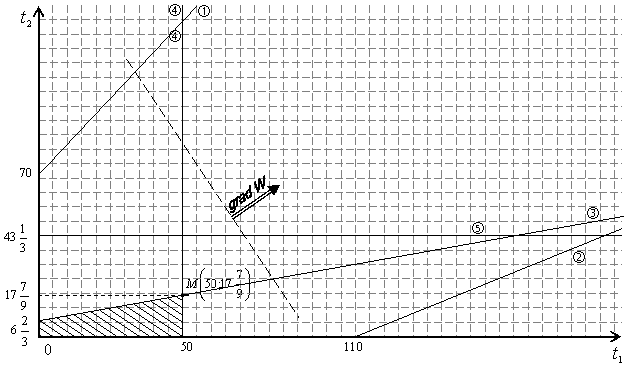
Эту задачу с двумя переменными можно решить графически:
График 1.
На графике видно, что система линейных неравенств (3.4), (3.5), образует
область допустимых решений, ограниченную прямыми:
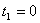 , , 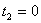 , , 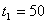 , , 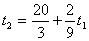 при этом линии уровня функции (3.1) перпендикулярны вектору-градиенту
при этом линии уровня функции (3.1) перпендикулярны вектору-градиенту 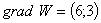 и образуют семейство параллельных прямых (градиент указывает направление
возрастания функции). Наибольшего значения функция (3.1) достигает в точке
и образуют семейство параллельных прямых (градиент указывает направление
возрастания функции). Наибольшего значения функция (3.1) достигает в точке  пересечения прямых:
пересечения прямых:
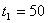 и и 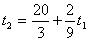 Координаты этой точки и определяют искомые объемы дополнительных ресурсов.
Следовательно, программа «расшивки узких мест производства имеет вид:
Координаты этой точки и определяют искомые объемы дополнительных ресурсов.
Следовательно, программа «расшивки узких мест производства имеет вид:
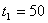 , , 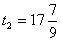 , , 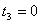 и прирост прибыли составит:
и прирост прибыли составит:
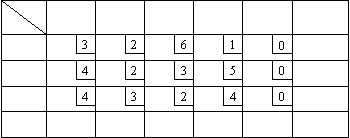
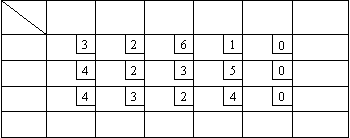
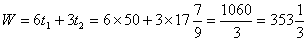 Сводка результатов по пунктам 1-3 приведена в таблице 2.
Сводка результатов по пунктам 1-3 приведена в таблице 2.
Таблица 2. | | 
| 30 | 11 | 45 | 6 | B | 
| 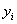
| 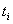
| 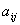
| 3 | 2 | 6 | 0 | 150 | 0 | 6 | 50 | | 4 | 2 | 3 | 5 | 130 | 0 | 3 | 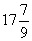
| | 4 | 3 | 2 | 4 | 124 | 8 | 0 | 0 | 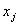
| 22 | 0 | 14 | 0 | 1290 | | | 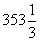
| 
| 0 | 7 | 0 | 9 | | | | | | | | | | | | | | |
4. Транспортная задача
Транспортная задача – это задача о минимизации транспортных расходов,
связанных с обеспечением пунктов потребления определенным количеством
однородной продукции, производимой (хранимой) в нескольких пунктах
производства (хранения). В общем виде задача может быть сформулирована
следующим образом:
Однородный продукт, сосредоточенный в 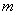 пунктах производства (хранения), необходимо распределить между
пунктах производства (хранения), необходимо распределить между 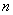 пунктами потребления. Стоимость перевозки единицы продукции известна для всех
маршрутов. Необходимо составить такой план перевозок, при котором запросы всех
пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах
производства и общие транспортные расходы по доставке продуктов были бы
минимальными.
Примем следующие обозначения:
пунктами потребления. Стоимость перевозки единицы продукции известна для всех
маршрутов. Необходимо составить такой план перевозок, при котором запросы всех
пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах
производства и общие транспортные расходы по доставке продуктов были бы
минимальными.
Примем следующие обозначения:
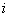
| Номер пункта производства (хранения) (i=1,2,.,m) | 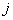
| Номер пункта потребления (j=1,2,.,n) | 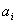
| Количество продукта, имеющиеся в i-ом пункте производства | 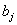
| Количество продукта, необходимое для j-го пункта потребления | 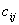
| Стоимость перевозки единицы продукта из i-го пункта отправления в j-ый пункт назначения | 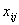
| Количество груза, планируемого к перевозке от i-го пункта отправления в j-ый пункт назначения |
Тогда, при наличии баланса производства и потребления:
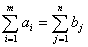 математическая модель транспортной задачи будет выглядеть следующим образом:
найти план перевозок
математическая модель транспортной задачи будет выглядеть следующим образом:
найти план перевозок
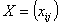 , где , где 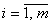 ; ; 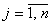 минимизирующий общую стоимость всех перевозок
минимизирующий общую стоимость всех перевозок
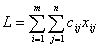 при условии, что из любого пункта производства вывозиться весь продукт
при условии, что из любого пункта производства вывозиться весь продукт
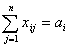 , где , где 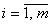
| (4.1) |
и любому потребителю доставляется необходимое количества груза
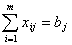 , где , где 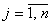
| (4.2) |
причем, по смыслу задачи
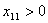 , ., , ., 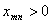 Для решения транспортной задачи чаще всего применяется метод потенциалов, при
котором вводят обозначение вектора симплексных множителей или потенциалов:
Для решения транспортной задачи чаще всего применяется метод потенциалов, при
котором вводят обозначение вектора симплексных множителей или потенциалов:
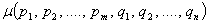 Тогда:
Тогда:
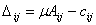 , где , где 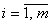 ; ; 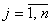 Откуда следует:
Откуда следует:
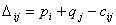 , где , где 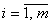 ; ; 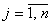 При этом один из потенциалов можно выбирать произвольно, т.к. в системе (4.1) и
(4.2) одно уравнение линейно зависит от остальных, а остальные потенциалы
находятся, что для базисных значений
При этом один из потенциалов можно выбирать произвольно, т.к. в системе (4.1) и
(4.2) одно уравнение линейно зависит от остальных, а остальные потенциалы
находятся, что для базисных значений 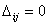 .
Предположим, что однородный продукт, находящийся в трех пунктах производства
(m=3), необходимо доставить в четыре пункта потребления (n=4). При этом
матрица
.
Предположим, что однородный продукт, находящийся в трех пунктах производства
(m=3), необходимо доставить в четыре пункта потребления (n=4). При этом
матрица 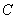 транспортных затрат на перевозку единицы продукта из любого пункта отправления в
любой пункт назначения, вектор
транспортных затрат на перевозку единицы продукта из любого пункта отправления в
любой пункт назначения, вектор 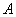 объемов запасов продукта в пунктах производства и вектор
объемов запасов продукта в пунктах производства и вектор 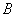 объемов продукта, необходимых пунктам потребления, имеют вид:
Тогда получается, что общий объем продукта в пунктах производства
объемов продукта, необходимых пунктам потребления, имеют вид:
Тогда получается, что общий объем продукта в пунктах производства
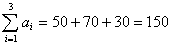 больше, чем
требуется всем потребителям больше, чем
требуется всем потребителям 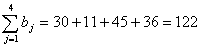 , т.е. имеем открытую модель транспортной задачи.
Для того чтобы превратить открытую модель транспортной задачи в закрытую,
необходимо ввести фиктивный пункт потребления с объемом потребления
, т.е. имеем открытую модель транспортной задачи.
Для того чтобы превратить открытую модель транспортной задачи в закрытую,
необходимо ввести фиктивный пункт потребления с объемом потребления
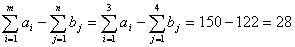 единиц,
при этом тарифы на перевозку продукта в этот пункт потребления будут равны
нулю, т.к. фактического перемещения продукта не происходит.
Тогда, первое базисное допустимое решение легко построить по правилу
«северо-западного угла». А т.к. оценки базисных клеток транспортной таблицы
равны нулю, то, приняв, что единиц,
при этом тарифы на перевозку продукта в этот пункт потребления будут равны
нулю, т.к. фактического перемещения продукта не происходит.
Тогда, первое базисное допустимое решение легко построить по правилу
«северо-западного угла». А т.к. оценки базисных клеток транспортной таблицы
равны нулю, то, приняв, что 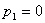 , первая транспортная таблица и потенциалы имеют вид:
, первая транспортная таблица и потенциалы имеют вид:
| 
| 30 | 11 | 45 | 36 | 28 | | 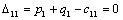
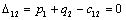
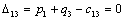
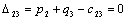
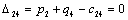
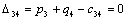
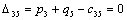
| 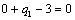
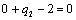
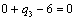
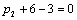
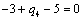
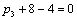
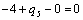
|  50 50
| 30 | 11 | 9 | * | | 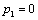
| | 70 | | | 36 | 34 | | 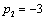
| | 30 | | | | 2 | 28 | 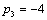
| | 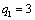
| 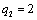
| 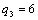
| 
| 
| |
Т.к. наибольшая положительная оценка всех свободных клеток транспортной
таблицы, соответствует клетке 14, то строим цикл пересчета: 14-13-23-24 и
производим перераспределение поставок вдоль цикла пресчета:
То получаем второе базисное допустимое решение и находим новые потенциалы,
полагая 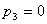 : :
 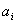
| 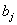
| 30 | 11 | 45 | 36 | 28 | | 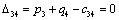
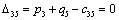
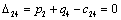
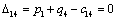
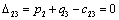
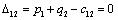
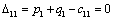
| 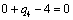
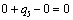
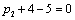
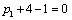
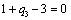
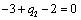
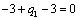
|  50 50
| 30 | 11 | | 9 | | 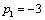
| | 70 | | * | 45 | 25 | | 
| | 30 | | | | 2 | 28 | 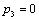
| | 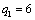
| 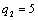
| 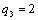
| 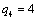
| 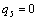
| |
Т.к. теперь наибольшая положительная оценка всех свободных клеток
транспортной таблицы, соответствует клетке 22, то строим цикл пересчета:
22‑12‑14‑24 и производим перераспределение поставок вдоль
цикла пресчета:
Отсюда получаем третье базисное допустимое решение и находим новые потенциалы,
принимая 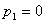 : :
 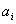
| 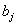
| 30 | 11 | 45 | 36 | 28 | | 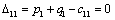
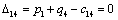
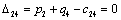
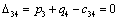
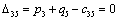
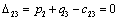
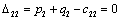
| 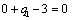
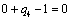
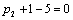
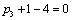
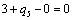
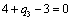
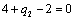
|  50 50
| 30 | | | 20 | | 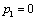
| | 70 | * | 11 | 45 | 14 | | 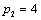
| | 30 | | | | 2 | 28 | 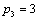
| | 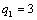
| 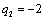
| 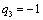
| 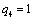
| 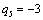
| |
Т.к. наибольшая положительная оценка всех свободных клеток транспортной
таблицы, теперь соответствует клетке 21, то строим цикл пересчета: 21-11-14-
24 и производим перераспределение поставок вдоль цикла пресчета:
Страницы: 1, 2, 3, 4
|
|
|
|
|