|
|
|
|
Курсовая: Динамическое и линейное программирование
Получаем четвертое базисное допустимое решение и находим новые потенциалы,
принимая 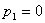 : :
 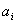
| 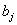
| 30 | 11 | 45 | 36 | 28 | | 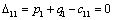
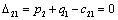
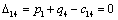
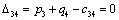
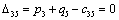
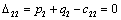
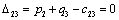
| 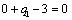
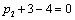
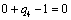
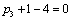
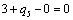
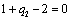
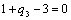
|  50 50
| 16 | | | 34 | | 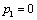
| | 70 | 14 | 11 | 45 | | | 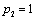
| | 30 | | | * | 2 | 28 | 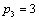
| | 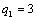
| 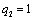
| 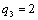
| 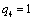
| 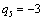
| |
Т.к. наибольшая положительная оценка всех свободных клеток транспортной
таблицы, соответствует клетке 33, то строим цикл пересчета: 33-23-21-
11‑14‑34 и производим перераспределение поставок вдоль цикла
пресчета:
Получаем пятое базисное допустимое решение и находим новые потенциалы, опять
принимая 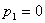 : :
 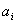
| 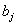
| 30 | 11 | 45 | 36 | 28 | | 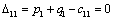
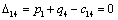
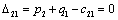
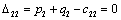
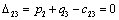
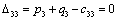
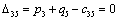
| 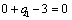
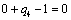
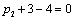
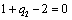
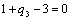
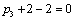
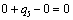
| | 50 | 14 | | | 36 | | 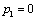
|  70 70
| 16 | 11 | 43 | | * | 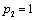
| | 30 | | | 2 | | 28 | 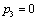
| | 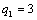
| 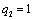
| 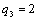
| 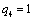
| 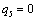
| |
Теперь наибольшая положительная оценка всех свободных клеток транспортной
таблицы, соответствует клетке 25, отсюда строим цикл пересчета: 25-23-33- и
производим перераспределение поставок вдоль этого цикла пресчета:
Получаем пятое базисное допустимое решение и снова находим новые потенциалы,
принимая 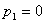 : :
 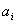
| 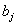
| 30 | 11 | 45 | 36 | 28 | | 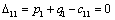
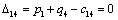
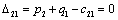
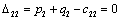
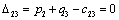
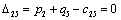
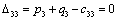
| 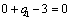
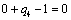
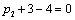
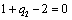
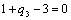
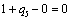
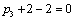
| | 50 | 14 | | | 36 | | 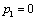
| | 70 | 16 | 11 | 15 | | 28 | 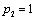
| | 30 | | | 30 | | | 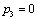
| | 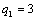
| 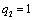
| 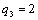
| 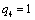
| 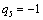
| |
Находим оценки всех свободных клеток таблицы:
Т.к. получили таблицу для которой нет ни одной положительной оценки,
следовательно, найдено оптимальное базисное допустимое решение:
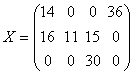 при котором транспортные расходы по обеспечению продуктом всех четырех пуктов
потребления будут наименьшими. При этом из второго пункта производства товар
будет вывезен не полностью, т.е. там останется остаток продукта 28 единиц.
при котором транспортные расходы по обеспечению продуктом всех четырех пуктов
потребления будут наименьшими. При этом из второго пункта производства товар
будет вывезен не полностью, т.е. там останется остаток продукта 28 единиц.
5. Распределение капитальных вложений
Задача о распределении капитальных вложений – это нелинейная задача
распределения ресурсов между предприятиями одного производственного
объединения или отрасли.
Предположим, что указано 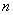 пунктов, где требуется построить или реконструировать предприятия одной отрасли,
для чего выделена определенная сумма. При этом известен прирост мощности или
прибыли для каждого предприятия, в зависимости от суммы капитальных вложений в
это предприятие. Требуется найти такое распределение капитальных вложений между
предприятиями, которое максимизирует суммарный прирост мощности или прибыли
всей отрасли.
Примем следующие обозначения:
пунктов, где требуется построить или реконструировать предприятия одной отрасли,
для чего выделена определенная сумма. При этом известен прирост мощности или
прибыли для каждого предприятия, в зависимости от суммы капитальных вложений в
это предприятие. Требуется найти такое распределение капитальных вложений между
предприятиями, которое максимизирует суммарный прирост мощности или прибыли
всей отрасли.
Примем следующие обозначения:
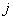
| Номер предприятия (j=1,2,.,n) | 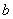
| Общая сумма капитальных вложений | 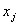
| Сумма капитальных вложений в j-ое предприятие | 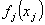
| Прирост мощности или прибыли j-го предприятия, если оно получит xj денежных единиц капитальных вложений |
Тогда, задача состоит в том, чтобы найти такие значения 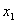 ,
, 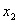 , ., , ., 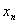 , при которых значение суммарного прироста прибыли или мощности всей отрасли:
, при которых значение суммарного прироста прибыли или мощности всей отрасли:
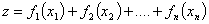 было бы наибольшим, при ограничении общей суммы:
было бы наибольшим, при ограничении общей суммы: 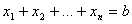 , причем будем считать, что все переменные
, причем будем считать, что все переменные 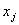 принимают только целые неотрицательные значения, т.е.:
принимают только целые неотрицательные значения, т.е.:
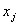 =0 или 1, или 2, или 3, .; =0 или 1, или 2, или 3, .; 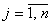 Эту задачу можно решить методом динамического программирования. Для этого
необходимо ввести параметр состояния
Эту задачу можно решить методом динамического программирования. Для этого
необходимо ввести параметр состояния 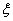 и функцию состояния
и функцию состояния 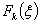 :
:
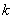
| Некоторое количество предприятий, для которых определяется параметр и функция состояния (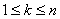 ) ) | 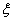
| Сумма капитальных вложений, выделяемая нескольким предприятиям (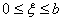 ) ) | 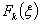
| Максимальный прирост прибыли или мощности на первых 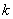 предприятиях, если они вместе получат предприятиях, если они вместе получат 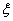 капитальных вложений капитальных вложений |
Тогда, если из 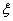 денежных единиц k-ое предприятие получит
денежных единиц k-ое предприятие получит 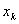 денежных единиц, то остаток
денежных единиц, то остаток 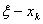 денежных средств необходимо распределить между предприятиями от первого до
денежных средств необходимо распределить между предприятиями от первого до 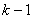 так, чтобы был получен максимальный прирост прибыли или мощности
так, чтобы был получен максимальный прирост прибыли или мощности 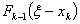 . Следовательно, прирост прибыли или мощности k предприятий будет равен
. Следовательно, прирост прибыли или мощности k предприятий будет равен 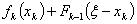 и нужно выбрать такое значение
и нужно выбрать такое значение 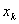 между 0 и
между 0 и 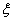 , чтобы
увеличение прибыли или мощности k предприятий было бы максимальным,
т.е.: , чтобы
увеличение прибыли или мощности k предприятий было бы максимальным,
т.е.:
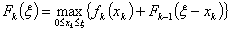 , где , где 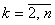 .
Если же k=1, то: .
Если же k=1, то:
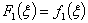 Допустим, что производственное объединение состоит из четырех предприятий (n
=4). Общая сумма капитальных вложений равна 700 денежных единиц (b=700),
при этом суммы выделяемые предприятиям кратны 100 денежным единицам. Значения
функций
Допустим, что производственное объединение состоит из четырех предприятий (n
=4). Общая сумма капитальных вложений равна 700 денежных единиц (b=700),
при этом суммы выделяемые предприятиям кратны 100 денежным единицам. Значения
функций 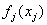 приведены
в таблице 3: приведены
в таблице 3:
Таблица 3. | 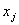
| 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 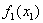
| 0 | 42 | 58 | 71 | 80 | 89 | 95 | 100 | 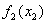
| 0 | 30 | 49 | 63 | 68 | 69 | 65 | 60 | 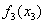
| 0 | 22 | 37 | 49 | 59 | 68 | 76 | 82 | 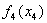
| 0 | 50 | 68 | 82 | 92 | 100 | 107 | 112 |
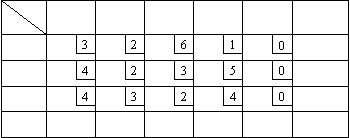
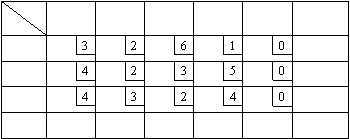
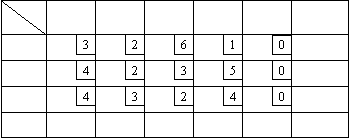
Для заполнения таблицы 5 необходимо в таблице 4 сложить значения функции 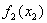 со значениями
со значениями 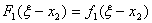 и на
каждой северо-восточной диагонали выбрать наибольшее число (отмечено
звездочкой), указав соответствующие значение и на
каждой северо-восточной диагонали выбрать наибольшее число (отмечено
звездочкой), указав соответствующие значение 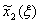 :
:
Страницы: 1, 2, 3, 4
|
|
|
|
|

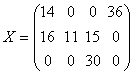 при котором транспортные расходы по обеспечению продуктом всех четырех пуктов
потребления будут наименьшими. При этом из второго пункта производства товар
будет вывезен не полностью, т.е. там останется остаток продукта 28 единиц.
при котором транспортные расходы по обеспечению продуктом всех четырех пуктов
потребления будут наименьшими. При этом из второго пункта производства товар
будет вывезен не полностью, т.е. там останется остаток продукта 28 единиц.

 50
50