|
РУБРИКИ |
Статья: Морфологический анализ цветных (спектрозональных) изображений |
РЕКОМЕНДУЕМ |
||
|
Статья: Морфологический анализ цветных (спектрозональных) изображенийздесь индикаторные функции непересекающихся подмножеств Аi, i=1,....,N, положительной меры поля зрения Х, на каждом из которых функции , j=1,...,n, i=1,...,N, непрерывны. Поскольку согласно лемме 2 то цветное изображение fe(×), такого объекта характеризует его форму непрерывным распределением яркости и цвета на каждом подмножестве Ai, i=1,...,N. Для изображения где характерно напрерывное распределение яркости и цвета на каждом Ai , если непрерывные функции. Если, в частности, цвет и яркость постоянны на Ai, i=1,...,N, то это верно и для всякого изображения , если явно от Для такого изображения примем следующее представление: , (4) его черно-белый вариант на каждом Ai имеет постоянную яркость не меняется на Ai и равен Поскольку для реальных изображений должно быть выполнено условие физичности (2*), форму изображения (4), имеющего на различных множествах Аi имеет несовпадающие яркости и различные цвета определим как выпуклый замкнутый в конус: v(a), очевидно, содержится в n×N мерном линейном подпространстве которое назовем формой a(×) в широком смысле. Форму в широком смысле любого изображения a(×), у которого не обязательно различны яркости и цвета на различных подмножествах Ai ,i=1,...,N, определим как линейное подпространство , натянутое не вектор-функции Fa(×),FÎF, где F - класс преобразований , определенных как преобразования векторов a(x)®Fa(x) во всех точках xÎX; здесь F - любое преобразование . Тот факт, что F означает как преобразование , так и преобразование , не должен вызывать недоразумения. Изображения из конуса(4***) имеют форму, которая не сложнее, чем форма a(×) (4), поскольку некоторые из них могут иметь одно и то же значение яркости или(и) цвета на различных множествах Аi, i=1,......,N. Также множества оказываются, по существу, объединенными в одно, что и приводит к упрощению формы изображения, поскольку оно отражает меньше деталей формы изображенного объекта, чем изображение (4). Это замечание касается и L(a(×)), если речь идет о форме в широком смысле. Лемма 3. Пусть {Аi} - измеримое разбиение X: Изображение (3) имеет на каждом подмножестве Ai : - постоянную яркость - постоянный цвет , если и только если в (3) ; - постоянную яркость fi , i=1,...,N, если и только если в (3) не зависит от i=1,....,N. Доказательство . На множестве Ai яркость и цвет изображения (3) равны соответственно[6] Если выполнено равенство (4), то и не зависят. Наоборот, если и , т.е. выполняется (4). Если не зависит от Наоборот, пусть не зависит от силу линейной независимости координаты j(i)(x) не зависят от , т.е. следовательно, где A i и . Последнее утверждение очевидно n Цвет изображения определяется как электродинамическими свойствами поверхности изображенного объекта, так и спектральным составом облучающего электромагнитного излучения в том диапазоне, который используется для регистрации изображения. Речь идет о спектральном составе излучения, покидающего поверхность объекта и содержащего как рассеянное так и собственное излучения объекта. Поскольку спектральный состав падающего излучения, как правило, пространственно однороден, можно считать, что цвет изображения несет информацию о свойствах поверхности объекта, о ее форме, а яркость в значительной степени зависит и от условий “освещения”. Поэтому на практике в задачах морфологического анализа цветных изображений сцен важное значение имеет понятие формы изображения, имеющего постоянный цвет и произвольное распределение яркости в пределах заданных подмножеств Ai , i=1,...,N, поля зрения X. Итак, пусть в согласии с леммой 3 где, в пределах Ai при постоянном цвете причем для изображения (5) цвета j(i), i=1,....,N, считаются попарно различными, а функции g(i), i=1,....,N, - удовлетворяющими условиям i=1,....,N. Нетрудно заметить, что в выражениях (5),(6) и (7) без потери общности можно принять условие нормировки , позволяющее упростить выражения (6) и (7) для распределений яркости и цвета. С учетом нормировки распределение яркости на Ai задается функцией на Ai равен Форму изображения (5) определим как класс всех изображений (8) каждое из которых, как и изображение (5), имеет постоянный цвет в пределах каждого Ai, i=1,...,N. Форма таких изображений не сложнее, чем форма f(×) (5), поскольку в изображении на некоторых различных подмножествах Ai, i=1,...,N, могут совпадать значения цвета, которые непременрно различны в изображении f (×) (5). Совпадение цвета на различных подмножествах Ai, i=1,...,N ведет к упрощению формы изображения по сравнению с формой f(×) (5). Все изображения , имеющие различный цвет на различных Ai, i=1,...,N, считаются изоморфными f(×) (и между собой), форма остальных не сложнее, чем форма f(×). Если , то, очевидно, Если в (8) яркость , то цвет i считается произвольным (постоянным), если же в точках некоторого подмножества , то цвет i считается равным цвету на Цвет изображения (8) может не совпадать с цветом (5). Если же по условию задачи все изображения форма которых не сложнее, чем форма , должны иметь на Ai, i=1,...,N, тот же цвет, что и у то следует потребовать, чтобы , в то время, как яркости остаются произвольными (если , то цвет i определяется равным цвету f(×) на A i, i=1,...,N). Нетрудно определить форму любого, не обязательно мозаичного, изображения f(×) в том случае, когда допустимы произвольные изменения яркости неизменном цвете j(x) в каждой точке . Множество, содержащее все такие изображения назовем формой в широком смысле изображения , у которого f(x)¹0, m-почти для всех , [ср. 2]. линейным подпространством , содержащем любую форму в которой включение определяет допустимые значения яркости. В частности, если означает, что яркость неотрицательна: , то замкнутый конус в принадлежащий Более удобное описание формы изображения может быть получено на основе методов аппроксимации цветных изображений, в которых форма определяется как оператор наилучшего приближения. В следующем параграфе дано представление формы изображения в виде оператора наилучшего приближения. 5. Задачи аппроксимации цветных изображений. Форма как оператор наилучшего приближения. Рассмотрим вначале задачи приближения кусочно-постоянными (мозаичными) изображениями. Решение этих задач позволит построить форму изображения в том случае, когда считается, что для любого преобразования , действующего на изображение как на вектор каждой точке оставляющего элементом изображением. Форма в широком смысле определяется как оператор наилучшего приближения изображения изображениями где а наилучшего приближения элементами множества , форма которых не сложнее, чем форма . Характеристическим для является тот факт, что, если f(x)=f(y), то для любого 5.1. Приближение цветного изображения изображениями, цвет и яркость которых постоянны на подмножествах разбиения поля зрения X. Задано разбиение , требуется определить яркость и цвет наилучшего приближения на каждом . Рассмотрим задачу наилучшего приближения в цветного изображения f(×) (2) изображениями (4), в которых считается заданным разбиение поля зрения X и требуется определить из условия (11) Теорема 1. Пусть и искомое изображение (4) задается равенством . (13) Оператор является ортогональным проектором на линейное подпространство (4****) изображений (4), яркости и цвета которых не изменяются в пределах каждого Ai , i=1,...,N. Черно-белый вариант (4*) цветного изображения (4) является наилучшей в аппроксимацией черно-белого варианта цветного изображения f(×) (2), если цветное изображение является наилучшей в аппроксимацией цветного изображения f(×) (2). Оператор является ортогональным проектором на линейное подпространство черно-белых изображений, яркость которых постоянна в пределах каждого . В точках множества цвет наилучшей аппроксимации (4) цветного изображения f(×) (2) является цветом аддитивной смеси составляющих f(×) излучений, которые попадают на . Доказательство. Равенства (12) - условия минимума положительно определенной квадратичной формы (11), П - ортогональный проектор, поскольку в задаче (11) наилучшая аппроксимация - ортогональная проекция f(×) на . Второе утверждение следует из равенства ,i=1,...,N вытекающих из (12) и равенства (1), в котором индекс k следует заменить на xÎX. ■ Замечание 1. Для любого измеримого разбиения ортогональные проекторы и соответственно форму в широком смысле цветного изображения (4), цвет и яркость которого, постоянные в пределах каждого , различны для различных , ибо форму в широком смысле черно-белого изображения, яркость которого постоянна на каждом для разных ,[2]. Если учесть, условие физичности (2*), то формой цветного изображения следует считать проектор на выпуклый замкнутый конус (4***) Аналогично формой черно-белого изображения следует считать проектор на выпуклый замкнутый конус изображений (4*), таких, что [2]. Дело в том, что оператор определяет форму изображения (4), а именно |
|
© 2010 |
|
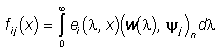 ,
, 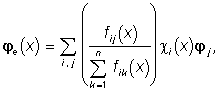
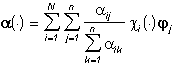 (4**)
(4**)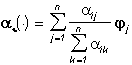 , i=1,...,N.
, i=1,...,N.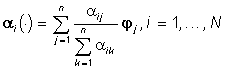 ,
,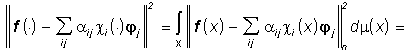
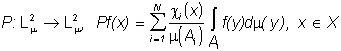 ,
,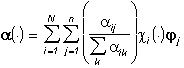 (4**)
(4**)