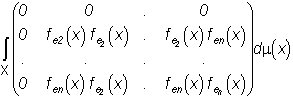|
РУБРИКИ |
Статья: Морфологический анализ цветных (спектрозональных) изображений |
РЕКОМЕНДУЕМ |
||
|
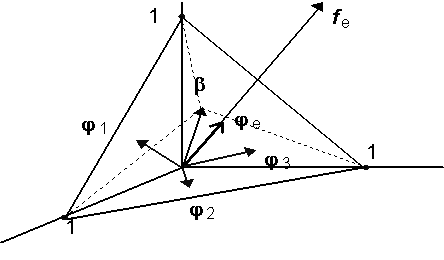
Статья: Морфологический анализ цветных (спектрозональных) изображенийв котором Поскольку в задаче наилучшего приближения f(×) изображениями этого класса предстоит найти , векторы i=1,...,N, можно считать ортогональными, определив , (*) из условия минимума невязки по . После этого для каждого i=1,...,N векторы должны быть определены из условия при дополнительном условии ортогональности Лемма 5. Пусть ортогональные собственные векторы оператора Фi (23), упорядоченные по убыванию собственных значений: Тогда решение задачи (**) дается равенствами Доказательство. Заметим, что, поскольку Фi - самосопряженный неотрицательно определенный оператор, его собственные значения неотрицательны, а его собственные векторы всегда можно выбрать так, чтобы они образовали ортогональный базис в Rn. Пусть P i - ортогонально проецирует в Rn на линейную оболочку собственных векторов и [Pi Фi Pi] - сужение оператора P i Фi Pi на . Тогда левая часть (*) равна следу оператора [Pi Фi P i] - j-ое собственное значение оператора (см., например, [10]). Пусть . Тогда согласно теореме Пуанкаре, [10], , откуда следует утверждаемое в лемме. ■ Воспользовавшись выражениями (*) и леммой 5, найдем, что в рассматриваемом случае имеет место утверждение, аналогичное теореме 3. Теорема 3*. Наилучшее приближение любого изображения f (×) изображениями (17*) имеет вид Где . Невязка наилучшего приближения равна Рассмотрим теперь задачу наилучшего приближения изображения f (×) изображениями (17), в которых заданы и фиксированы векторы , и надлежит определить измеримое разбиение и функции решение задачи При любом разбиении минимум в (30) по достигается при определяемых равенством (20). В свою очередь, очевидно, что (31) где точки которых выполняется равенство могут быть произвольно включены в одно из множеств : либо в , либо в соглашение отмечено звездочкой в (31). Таким образом доказана Теорема 6. Пусть где ортогональный проектор определен равенством (25), а - индикаторная функция множества (31), i=1,...,N. Невязка наилучшего приближения равна Замечание 5. Так как при то условия (31), определяющие разбиение показывающем, что множество в (32) инвариантно относительно любого преобразования изображения , не изменяющего его цвет. Теоремы 3 и 6 позволяют сформулировать необходимые и достаточные условия наилучшего приближения изображения f(×) изображениями (17), при котором должны быть найдены и ci0 , i=1,...,N, такие, что Теорема 7. Для заданного изображения f(×) определим множества равенствами (32), оператор П - равенством (24), - равенствами (25). Тогда , определено равенством (32), в котором - собственный вектор оператора Фi (23), отвечающий наибольшему собственному значению, причем в (23) , наконец, будет дано равенством (20), в котором , где собственный вектор оператора , отвечающий наибольшему собственному значению ; наконец, Замечание 6. Следующая итерационная процедура полезна при отыскании : Для изображения f(×) зададим и по теореме 5 найдем и теореме 3, используя найдем . После этого вновь воспользуемся теоремой 3 и по найдем и т.д. Построенная таким образом последовательность изображений очевидно обладает тем свойством, что числовая последовательность , k=1,2,.... монотонно не возрастает и, следовательно, сходится. К сожалению ничего определенного нельзя сказать о сходимости последовательности . Формы Теорема 7. Форма в широком смысле изображения определяется ортогональным проектором П*f : , при этом Доказательство. Так как для , то получаем первое утверждение. Для доказательства второго утверждения рассмотрим выпуклую задачу на минимум , решение которой определяется условиями (см., например, [11]) . Отсюда следует, что Замечание. Так как , где fi(x) - выходной сигнал i-го детектора в точке , причем fi(x)³0 ,i=1,...,n, и, следовательно цвет изображений непременно имеет неотрицательные , то для реальных изображений , условия , эквивалентны. Если же для некоторого , то условие влечет также, что для изображений g(×), удовлетворяющих условию , всегда Для спектрозональных изображений характерна ситуация, при которой k детекторов регистрируют рассеянную объектами солнечную радиацию в диапазоне видимого света, а остальные n-k регистрируют собственное тепловое излучение объектов ( в инфракрасном диапазоне). В таком случае любое изображение можно представить разложением В котором . Если ИК составляющей солнечного излучения можно пренебречь по сравнению с собственным излучением объектов, то представляет интерес задача приближения изображениями f(×) , в которых f1( ×) - любая неотрицательная функция из , j1(×) - фиксированное векторное поле цвета, f2(×) - термояркость, j2( ×) - термоцвет в точке . Форма П*f видимой компоненты f (×) (40) определяется как оператор наилучшего приближения в задаче , в данном случае *f действует фактически только на "видимую компоненту" g(×), обращая "невидимую, ИК, компоненту" g(×) в ноль. Форма ИК компоненты f(×) может быть определена лишь тогда, когда известно множество возможных преобразований j2( ×) f2(×). Некоторые применения. Задачи идентификации сцен. Рассмотрим вначале задачи идентификации сцен по их изображения, неискаженным геометрическими преобразованиями, поворотами, изменениями масштаба и т.д. Ограничимся задачами, в которых предъявляемые для анализа изображения получены при изменяющихся и неконтролируемых условиях освещения и неизвестных и, вообще говоря, различных оптических характеристиках сцены. 1). Задачи идентификации при произвольно меняющейся интенсивности освещения. Можно ли считать f(×) и g(×) изображениями одной и той же сцены, возможно, отличающимя лишь распределениями яркости, например, наличием теней? В простейшем случае для идентификации достаточно воспользоваться теоремой 5, а именно, f(×) и g(×) можно считать изображениями одной и той же сцены, если существует распределение цвета , для которого v(j(×)) содержит f(×) и g(×). Если , и существует котором f(x)Îv(j(×)), g(x )Îv(j(×)), а именно, , , , и, наконец, произвольно, если . На практике удобнее использовать другой подход, позволяющий одновременно решать задачи совмещения изображений и выделения объектов. Можно ли, например, считать g(×) изображением сцены, представленной изображением f (×)? Ответ следует считать утвердительным, если . Здесь j(×) - распределение цвета на изображении f (×), символ ~0 означает, что значение d(g(×)) можно объяснить наличием шума, каких-либо других погрешностей, или, наконец, - наличием или, наоборот, отсутствием объектов объясняющим несовпадение g (×) и f(×) с точностью до преобразования распределения яркостей. Такие объекты, изменившие распределение цвета g (×) по сравнению с распределением цвета f(×), представлены в 2).Идентификация при произвольном изменении распределения интенсивности и пространственно однородном изменении спектрального состава освещения. Можно ли считать изображением сцены, представленной на изображении f (×), изображение, полученное при изменившихся условиях регистрации, например, перемещением или изменением теней и изменением спектрального состава освещения? Пусть П - форма в широком смысле изображения f(×), определенная в теореме @, П* - форма f (×). Тогда ответ на поставленный вопрос можно считать утвердительным, если . Если изменение g(×) обусловлено не только изменившимися условиями регистрации, но также появлением и (или) исчезновением некоторых объектов, то изменения, обусловленные этим последним обстоятельством будут представлены на 3). Задачи совмещения изображений и поиска фрагмента. Пусть f(×) - заданное изображение, AÌX - подмножество поля зрения, cA(×) - его индикатор, c A(×)f(×) -назовем фрагментом изображения f(×) на подмножестве A, представляющем выделенный фрагмент сцены, изображенной на f(×). Пусть g (×) - изображение той же сцены, полученное при других условиях, в частности, например, сдвинутое, повернутое, т.е. геометрически искаженное по сравнению с f(×). Задача состоит в том, чтобы указать на g(×) фрагмент изображения, представляющий на f (×) фрагмент сцены и совместить его с cA(×)f (×). Ограничимся случаем, когда упомянутые геометрические искажения можно моделировать группой преобразований R2->R2, преобразование изображения назовем сдвигом g(×) на h. Здесь Q(h): Rn->Rn, hÎH, - группа операторов. Векторный сдвиг на h¢ÎH даст . В задаче выделения и совмещения фрагмента рассмотрим фрагмент сдвинутого на h изображения g(×) в “окне” A: (100) причем, поскольку где - ограничение на сдвиг “окна” А, которое должно оставаться в пределах поля зрения X. Если кроме цвета g(×) может отличаться от f (×), скажем, произвольным преобразованием распределения яркости при неизменном распределении цвета и - форма фрагмента f(×), то задача выделения и совмещения фрагмента сводится к следующей задаче на минимум .(101) При этом считается, что фрагмент изображения g(×), соответствующий фрагменту cA(×)f (×), будет помещен в “окно”.А путем соответствующего сдвига h=h *, совпадает с cA(×)f(×) с точностью до некоторого преобразования распределения яркости на нем. Это означает, что т.е. в (101) при h=h* достигается минимум. 4). В ряде случаев возникает следующая задача анализа спектрозональных изображений: выделить объекты которые “видны”, скажем, в первом канале и “не видны” в остальных. Рассмотрим два изображения и в широком смысле как множество всех линейных преобразований : линейный оператор R2->R2, не зависящий от xÎX). Для определения проектора на рассмотрим задачу на минимум . [*] Пусть , тогда задача на минимум [*] эквивалентна следующей: tr A*AS - 2trAB ~ . Ее решение (знаком - обозначено псевдообращение). Рис.1. fe - вектор выходных сигналов детекторов, отвечающий излучению e(×), je - его цвет; j1,j2,j 3, - векторы (цвета) базовых излучений, b - белый цвет, конец вектора b находится на пересечении биссектрис. Литература. [1] Пытьев Ю.П. Морфологические понятия в задачах анализа изображений, - Докл. АН СССР, 1975, т. 224, №6, сс. 1283-1286. [2] Пытьев Ю.П. Морфологический анализ изображений, - Докл. АН СССР, 1983, т. 296, №5, сс. 1061-1064. [3] Пытьев Ю.П. Задачи морфологического анализа изображений, - Математические методы исследования природных ресурсов земли из космоса, ред. Золотухин В.Г., Наука, Москва, 1984, сс. хххх-ххххх. [4] Пытьев Ю.П., Чуличков А.И. ЭВМ анализирует форму изображения, - Знание,сер. Математика, Кибернентика, Москва, 1988, 47 стр. [5] Yu.P.Pyt’ev. Morphological Image Analysis, Patt. Recogn. and Image Analysis, 1993, v.3, #1, pp.19-28. [6] Антонюк В.А., Пытьев Ю.П. Спецпроцессоры реального времени для морфологического анализа реальных сцен. Обработка изображений и дистанционное исследования, -Новосибирск, 1981, сс. 87-89. [7] Антонюк В.А., Пытьев Ю.П., Рау Э.И. Автоматизация визуального контроля изделий микроэлектроники,Радиотехника и электроника, 1985, т. ХХХ,№12, сс. 2456-2458. [8] Ермолаев А.Г., Пытьев Ю.П. Априорные оценки полезного сигнала для морфологических решающих алглритмов, - Автоматизация, 1984, №5, сс. 118-120. [9] Пытьев Ю.П, Задорожный С.С., Лукьянов А.Е. Об автоматизации сравнительного морфологического анализа электронномикроскопических изображений, - Изв. АН СССР, сер. физическая, 1977, т. 41, №11, сс. хххх- хххх. [10] A.A. Stepanov, S.Yu. Zheltov, Yu.V. Visilter. Shape analysis using Pyt'ev morphological paradigm and its using in machine vision. Proc. SPIE - Th. Intern. Soc. For Optical Engineering Videometrics III, 1994, v. 2350, pp. 163-167. [11] Пытьев Ю.П.. Математические методы интерпретации эксперимента, Высшая школа, 351 стр., 1989. [12] Майзель С.О. Ратхер Е.С. Цветовые расчеты и измерения. М:Л:Госэнергоиздат 1941, (Труды всесоюзного электротехнического института, вып.56). [13] P. Kronberg. Fernerkundung der Erde Ferdinand Enke. Verlag Stuthgart 1985. [1] Например, в связи с изменением времени суток, погоды, времени года и т.п. [2] Фрагмент морфологического анализа цветных изображений содержится в работе[3]. [3] вектор fe будет иметь отрицательные координаты, если он не принадлежит выпуклому конусу [4]черта символизирует замыкание, [5] Если - более детальное изображение , то некоторые A(j) могут “ращепиться” на несколько подмножеств A¢(j¢), на каждом из которых цвет постоянный, но различный на разных подмножествах A¢( j¢). Однако, поскольку форма обычно строится исходя из данного изображения f(×), v(f(×)) не может содержать изображения, которые более детально характеризуют изображенную сцену. [6] Для простоты яркость изображения считается положительной в каждой точке поля зрения Х. [7] [8]Одна и та же буква F использована как для оператора , так и для оператора . Эта вольность не должна вызывать недоразумения и часто используется в работе. [9]Если m(As)=0, то в задаче наилучшего приближения (18) цвет и распределение яркости на As можно считать произвольными, поскольку их значения не влияют на величину невязки s. [10]Векторы j1,..., j q выбираются, например, сообразно цветам объектов, представляющих интерес. |
|
© 2010 |
|
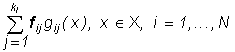
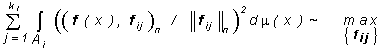 (**)
(**)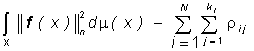 . n
. n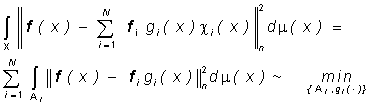 (30)
(30)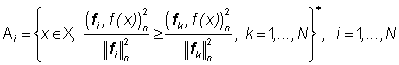 , (32)
, (32)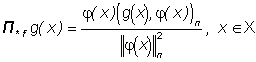 и
и 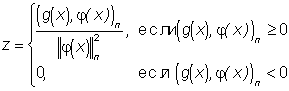 и тем самым доказано и второе утверждение n
и тем самым доказано и второе утверждение n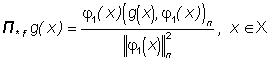 , причем П
, причем П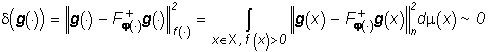
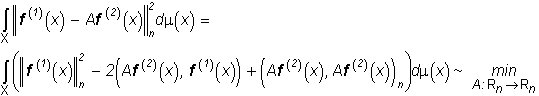
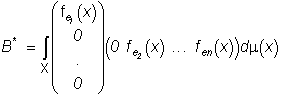 =
=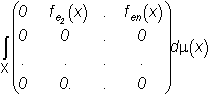
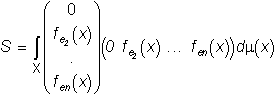 =
=