 |
РУБРИКИ |
Диплом: Организация познавательной деятельности учащихся на факультативных занятиях по теме Иррациональные неравенства |
РЕКОМЕНДУЕМ |
||
|
Диплом: Организация познавательной деятельности учащихся на факультативных занятиях по теме Иррациональные неравенстванапример, у Герона Александрийского находим: Для обозначения высших степеней употреблялись позже составные выражения "биквадрат" или "квадрато-квадрат" для четвертой степени, или "кубоквадрат" для пятой и т.д. Современные названия предложены голландским ученым С.Стевином (1548-1620), который обозначал степени в виде 2, 3 и т.д. Он же начал систематически употреблять дробные показатели степени для обозначения корней. В настоящее время для извлечения корня употребляется два обозначения: знак радикала и дробные показатели. Предпочтительнее использовать обозначения со знаком радикала - обозначения с дробными показателями являются скорее данью традиции. Степени с отрицательными показателями ввел английский математик Д.Уоллис. Неравенства встречаются в математике еще в глубокой ревности. Рассмотрим некоторые из них. 1. Среднее геометрическое двух положительных чисел меньше их среднего арифметического (Евклид). 2. Архимед установил неравенства 3. Если (Аль-Кальсади, Трактат "Раскрытие тайн науки Габар", XV век). Дальнейшие обобщения натуральных, целых, рациональных и т.д. чисел привели к понятию алгебраической системы, в частности, к понятию кольца и поля. Так, иррациональные числа с алгебраической точки зрения являются элементами поля , они не содержатся в поле , и поле расширением поля 2. Неравенства и их основные свойства Мы будем рассматривать положительные, отрицательные действительные числа и число . Изобразим горизонтальную числовую прямую, направленную вправо и числа на ней. При движении вдоль прямой слева направо числа будут появляться в порядке их возрастания. Ясно, что . Но точка, изображающая , расположена правее точки, изображающей . Таким образом, мы имеем следующее геометрическое правило для определения неравенства: Пусть - какие-нибудь два действительных числа, изображенных точками горизонтальной числовой прямой, направленной слева направо. Тогда в том и только том случае, когда точка, изображающая число , лежит правее точки, изображающей число . Это геометрическое правило можно заменить простым арифметическим правилом, если принять понятие положительного числа за основное: Пусть - какие-нибудь два действительных числа. Тогда в том и только том случае, когда положительно. В частности всякое положительное число больше нуля, ибо разность положительна. Поэтому неравенство употребляется для символической записи утверждения, что число положительно. Отрицательное число определяется как число, противоположное положительному числу относительно точки на числовой прямой. Всякое отрицательное число меньше нуля, ибо, если отрицательно, то положительно. Запись употребляется для обозначения утверждения, что отрицательное число. Число нуль обладает тем свойством, что Итак, числа 1). 2). 3). Причем всегда имеет место одно и только одно из этих соотношений. Рассмотрим теперь основные свойства неравенств. Теорема 1. Если и Это свойство называется свойством транзитивности неравенств. В самом деле, как сумма двух отрицательных слагаемых. Дадим геометрическое толкование свойства транзитивности: точка на числовой прямой расположена левее точки , а точка точки условиях точка расположена левее точки . Теорема 2. Если , то изменении знака обеих частей неравенства смысл знака неравенства меняется на обратный. Действительно, Следовательно, по определению Геометрическая иллюстрация: Теорема 3. Если и , т.е. обе части неравенства можно умножить на положительное число. Действительно, Но Теорема 4. Если и , т.е. при умножении на отрицательное число знак неравенства меняется на противоположный. Действительно, Но Теорема 5. Если и , т.е. при умножении обеих частей неравенства на нуль неравенство переходит в равенство. Действительно, Теорема 6. Если и число, то обеим частям неравенства можно прибавить произвольное число. Действительно, Теорема 7. Если , , то Предварительно напомним, что есть обратное число, т.е. такое, что . Имеем другой стороны, Следовательно, и так как, если произведение и один из множителей положительны, то и другой множитель положителен. Значит . Теорема 8. Если , то любого отличного от нуля числа положителен. Это следует из определения умножения положительных и отрицательных чисел. Теорема 9. Если и , т.е. два неравенства одинакового смысла можно сложить. Имеем или где Теорема 10. Если Теорема 11. (о перемножении неравенств) Если , и , т.е. обе части неравенства с положительными членами можно умножить на неравенство того же смысла, больший член которого положителен. Имеем последовательно: Здесь каждое произведение, а следовательно, и сумма положительны, что и требовалось доказать. Теорема 12. (о делении неравенств) Если Действительно, здесь , и, на основании теоремы о перемножении неравенств, имеем , что и требовалось доказать. Теорема 13. Если - четное число, , то степень любого числа, отличного от нуля, положительна. Теорема вытекает из положений, что Теорема 14. Если - нечетное число, и , т.е. отрицательное число в нечетной степени отрицательно. Теорема вытекает из следующих соотношений: |
|
© 2010 |
|
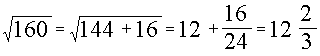
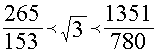
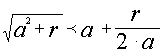 при
при 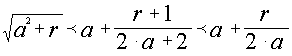 при
при 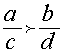 .
.